

In most streaming situations there’s no way to undo or change something we’ve already outputted-and we can’t wait until the stream ends, because it might be infinite-so we’re doomed. The first three coefficients are the same as what we’ve already outputted, but the fourth coefficient has changed from 14 to 4! Let’s say we receive the digit 3 next, so far giving us 1.433. So maybe we can safely emit these coefficients into our output stream and then keep emitting whatever coefficients come next? digits in 1.

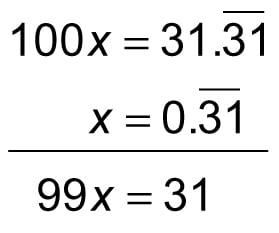
If we just truncate and compute 2 the continued fraction we get: 1.43 = Let’s say we’ve received the digits 1.43. It takes about 970 coefficients to get 1,000 digits for random numbers, but it takes 2,395 coefficients to get 1,000 digits of φ: We can see both of these behaviors by comparing φ to a few random streams of digits. But for the golden ratio it takes 2.39 coefficients to determine each decimal digit, the worst case 1 possible. Lochs’ theorem says that for almost all numbers, it takes 0.97 continued fraction coefficients on average to determine each decimal digit. One way to glimpse this is while converting its stream of continued fraction coefficients to digits-it takes many coefficients to get each digit: coefficients in 1 1 1 1 1 1 1 1 1 1 1 1 ⋮ digits out 1. One of the countless interesting things about the golden ratio is that it’s the “most irrational” number. Weight (Mass) to Volume to Converter for Recipes.Volume to (Weight) Mass Converter for Recipes.


 0 kommentar(er)
0 kommentar(er)
